⌂ Mathe-Training für die Oberstufe - Interaktive Lernprogramme

Mathe-Training für die Oberstufe - Bestimmung lokaler Extrempunkte (2. Verfahren)

Dieses Lernprogramm erklärt, wie man die lokalen Extrempunkte einer ganzrationalen Funktion mit Hilfe der 1. und 2. Ableitung ermittelt. Anschließend bietet es die Möglichkeit, das Verfahren kontrolliert zu üben.
Beispiel 1
✔
Beispiel 2 Übung
Aufgabe:
Bestimmen Sie rechnerisch die lokalen Extrempunkte des Graphen von f mit  f(x) = 0,1x3 - 0,15x2 - 1,8x + 1.
Erklärung
Verfahren
In allen lokalen Hoch- oder Tiefpunkten einer Funktion f ist die Tangente an den Graphen von f waagerecht, d. h. die Steigung der Tangente ist 0.
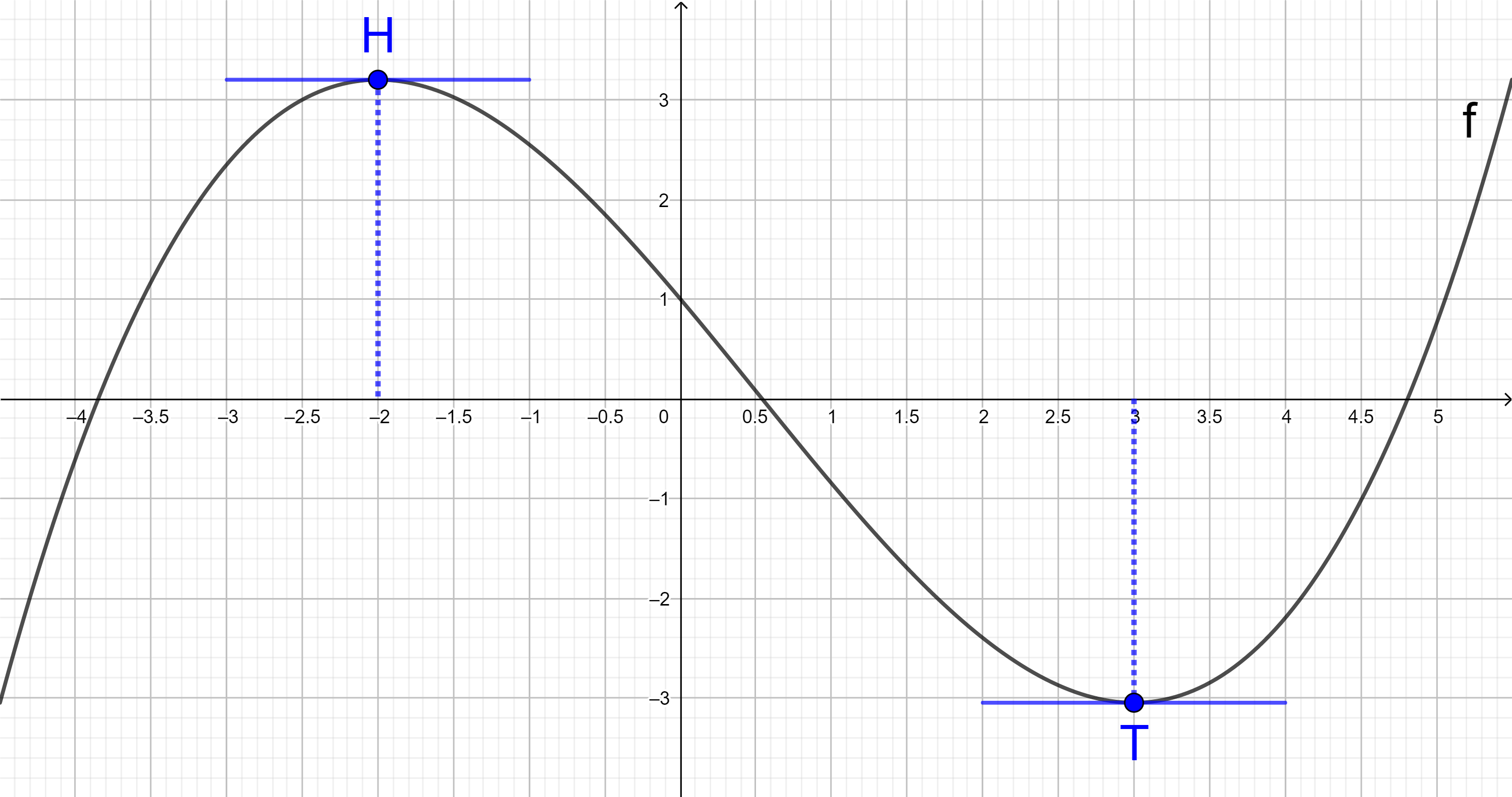
Die Steigung der Tangente wird mit der 1. Ableitung von f berechnet. Die x-Koordinate jedes Extrempunktes (genannt "Extremstelle") muss somit die Gleichung f '(x) = 0 erfüllen.
1. Schritt:
Bestimmung der möglichen Extremstellen
notwendige Bedingung:    f '(x) = 0
f '(x) = 0,3x2 - 0,3x - 1,8
(→ Lernprogramm "Ableitung ganzrationaler Funktionen", Kapitel 4.2. Ableitungsregeln)
0,3x2 - 0,3x - 1,8 = 0
Lösung der Gleichung mit dem GTR oder - wenn möglich - mit Hilfe geeigneter mathematischer Methoden (wie z. B. Ausklammern oder p,q-Formel)
Die möglichen Extremstellen lauten:
x1 = -2,   x2 = 3
Um herauszufinden, ob der Funktionsgraph an einer möglichen Extremstelle einen lokalen Hochpunkt oder einen lokalen Tiefpunkt hat, wird die Krümmung des Graphen untersucht.
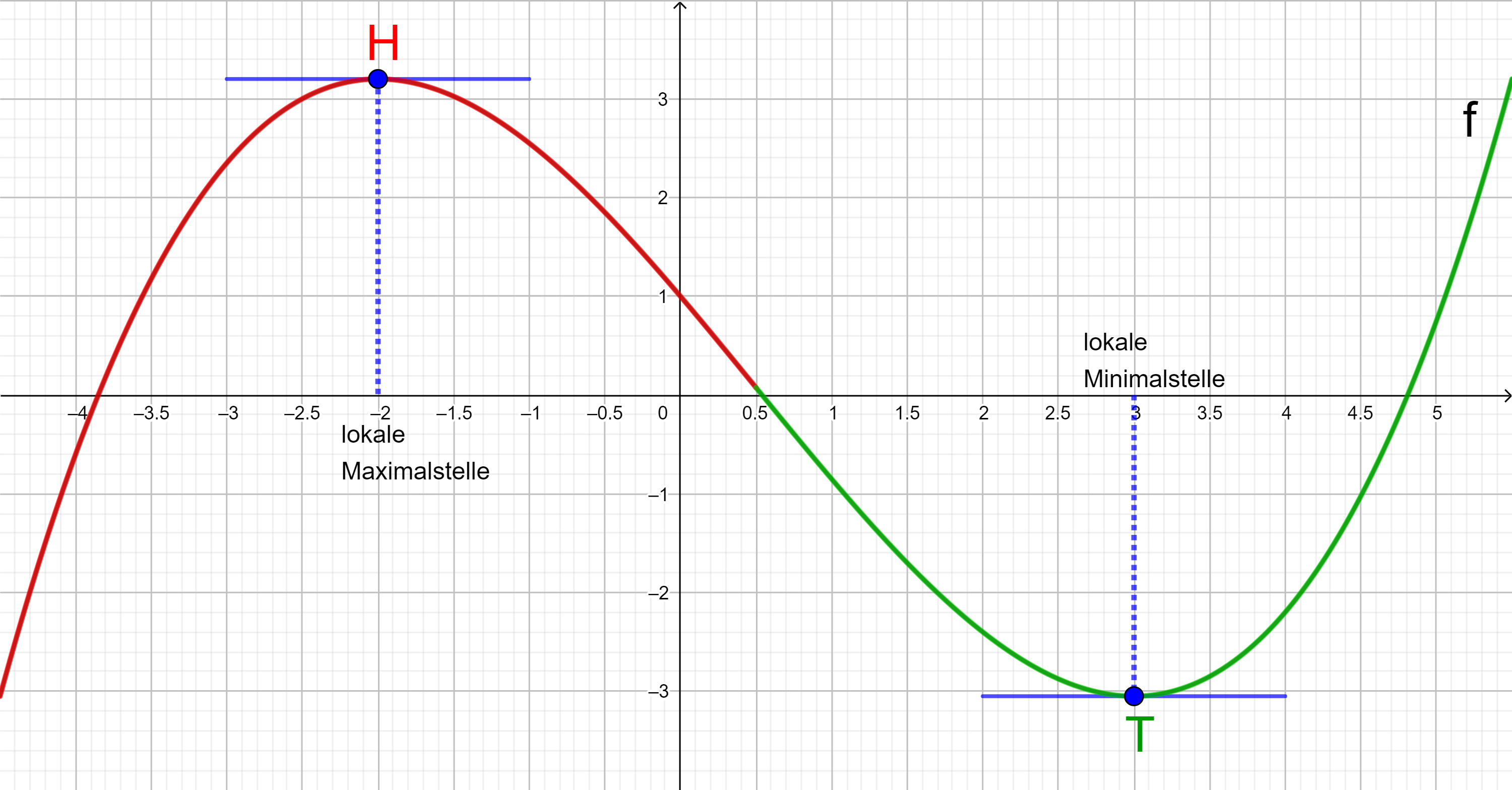
Ein lokaler Hochpunkt liegt auf einem rechtsgekrümmten Abschnitt des Funktionsgraphen, ein lokaler Tiefpunkt auf einem linksgekrümmten Abschnitt.
Bei einem rechtsgekrümmten Graphen nimmt die Steigung des Graphen kontinuierlich ab, bei einem linksgekrümmten kontinuierlich zu.
Die Änderung der Steigung im Verlauf des Funktionsgraphen kann mit Hilfe einer Animation veranschaulicht werden.
START
STOPP
RESET
→ Zeichnung
Der Graph der Ableitungsfunktion f ' (mit der die Steigung des Graphen von f berechnet wird) fällt in dem Intervall, in dem der Graph von f rechtsgekrümmt ist, und steigt in dem Intervall, in dem der Graph von f linksgekrümmt ist.
Mit der Ableitungsfunktion f '' wird die Steigung des Graphen von f ' berechnet.

Ist f ''(x) in einem Intervall negativ, fällt der Graph von f ' in diesem Intervall und der Graph von f ist rechtsgekrümmt.

Ist f ''(x) in einem Intervall positiv, steigt der Graph von f ' in diesem Intervall und der Graph von f ist linksgekrümmt.
Daraus ergibt sich ein hinreichendes Kriterium zur Bestimmung von Extremstellen:
Ist f '(x0) = 0 und f ''(x0) > 0,
hat der Graph von f an der Stelle x0 einen lokalen Tiefpunkt.
Ist f '(x0) = 0 und f ''(x0) < 0,
hat der Graph von f an der Stelle x0 einen lokalen Hochpunkt.
2. Schritt:
Untersuchung mit der 2. Ableitung
f ''(x) = 0,6x - 0,3
f ''(-2) = -1,5 < 0
Der Graph von f hat an der Stelle x1 = -2 einen lokalen Hochpunkt.
f ''(3) = 1,5 > 0
Der Graph von f hat an der Stelle x2 = 3 einen lokalen Tiefpunkt.
3. Schritt:
Angabe der lokalen Extrempunkte
f(-2) = 3,2 ( = lokales Maximum)
f(3) = -3,05 ( = lokales Minimum)
lokaler Hochpunkt:    H(-2 | 3,2)
lokaler Tiefpunkt:      T(3 | -3,05)